Archive for March 23rd, 2008

23 Mar

PDEs: Solving Simple PDEs Using Characteristics

Posted by S1TN in Math, Mathematics, PDEs.

Last time we derived a simple PDE describing the process of non-diffusive advection in a constantly flowing stream of water. That PDE looked like this: v\cdot u_x + u_t = 0, where v was the constant speed of the water. The solution of this PDE is a function of the form u(x,t).

This PDE follows a more general form that looks like this: c_2\cdot u_x + c_1\cdot u_t = 0, where c_1 and c_2 are constants. If you’ve studied multivariable calculus, you might recognize this kind of equation. It is, in fact, a directional derivative.

We can rewrite c_2 u_x + c_1 u_t = \nabla u \cdot \textbf{s} = 0, where \textbf{s} = (c_1, c_2). We can read this equation as “the gradient (or derivative) of u(x,t) in the direction of \textbf{s} is zero”. Which means that in the direction \textbf{s}, the solution u attains the same constant value. It may be easier to see by graphing it:

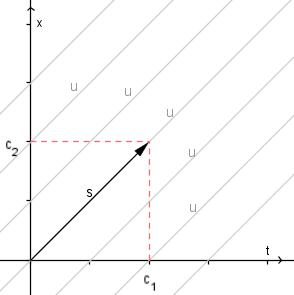
characteristics1.jpg

Continue reading →